兰兹伯格的初等物理教科书中,介绍了这样一个实验。
用带气孔的容器B(也可以用纸)盖住玻璃漏斗,漏斗颈的末端插入水中,再用一个玻璃容器A,从上方罩住密封的漏斗,然后,向容器A中吹进氢气。会看到,漏斗颈内部的水面向下降,最后,许多气泡从漏斗颈口逃出来。
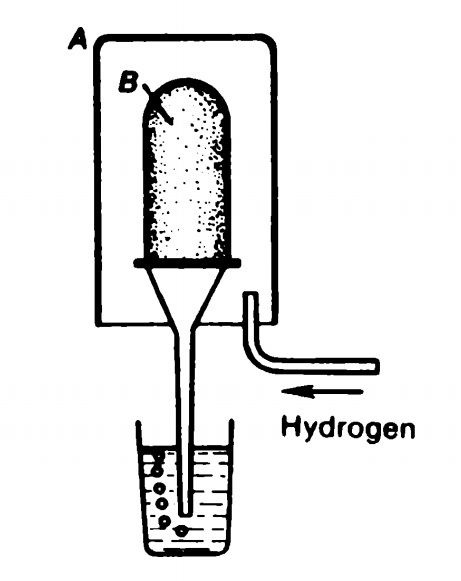
第一点:在上面介绍的实验中,容器A的下部是敞开的,与外面的空气连通。当连续向容器A中吹进氢气时,容器A内部原先的空气,以及后来的氢气,完全可以从A的下方跑掉呀。它们为什么搁着阳光大道不走,非要穿过带气孔的B(或纸)钻进漏斗中去呢?第二点:注意,实验中是将氢气吹进容器A。如果吹进的是空气,就观察不到任何现象。那么,怎样才能解释这个实验呢?不着急。
我们先来看一下,这个实验在书中的“出场背景”。它出现在13章“气体的性质”的第23节。第23节!?这意味着,在这之前,已经介绍了许许多多的事情。这还意味着,为了理解前面介绍的实验,需要具备许许多多的知识!确实如此。这一章在这个实验之前,都讲了哪些内容呢?
这一章是从“气体压强”开始的,它先向我们解释气体压强的含义与产生机制——用了两页多。然后介绍在体积保持固定时,气体压强随温度的变化(盖·吕萨克定律),在温度保持固定时,气体压强随体积的变化(波义耳定律,马略特定律),在压强保持固定时,气体体积随温度的变化(查理定律)。作者在介绍每一个定律时,都做了四件事:
(1)首先解释问题的含义(许多教科书都只给出问题,却不对问题的含义进行解释,好像对于学习者,问题的含义是自明和显然的。假如真是那样的话,他们还需要学习吗?);(2)详细介绍有关的实验;(3)然后才介绍,如何用公式和图形,把实验发现的定律表示出来;(4)最后给出对每一个定律的微观解释(用分子运动解释)。波义耳定律等几个定律,好像都很容易理解,没什么了不起。介绍它们,需要费这么大力气吗?有些人肯定这样疑惑。
有这种疑惑的人,很快就会从兰兹伯格的书学到:对貌似平凡的事情进行深入详尽的研究,会得出很重大的、意料之外的结果。因为,气体体积随温度的变化规律,使人们可以建立起一种新的温度标准,这就是热力学温标或绝对温标。采用新的温度标准后,气体体积以及气体密度与温度之间的关系,变得很简单。作者用了4节介绍与此有关的事情。这时候,终于能够去掉让压强、体积和温度三者之一保持不变的限制,建立起每种气体所满足的一般性状态方程。
气体状态方程,是针对单独一种气体的。对于由几种气体混合起来的气体,存在什么定律呢?作者紧接着给出了这种情况下的道尔顿定律。接着,作者把目光从气体体积转向气体密度。根据前面所讲的,气体的密度会随温度与压强而变化,所以,对不同气体的密度进行比较时,需要在相同的温度与压强条件下进行。而且,根据气体状态方程,只要在任一温度与任一压强下,测出一种气体的密度,就可以算出它在标准条件下的密度值来。这样就得到,不同气体在标准条件下的密度值。
这时候发现了一个极其重要的、事先不会料到的关系:气体的密度与气体的相对分子质量成正比!这就引出了阿伏伽德罗定律。这时发现,波义耳定律加上阿伏伽德罗定律,就可以解释道尔顿定律——它是前两者的必然结果。现在,作者把目光转向气体分子的运动速度。把盖·吕萨克定律与气体压强的微观起源结合起来,发现,绝对温度与气体分子的平均动能成正比。这样,在相同温度下,不同气体的分子运动速度(的平均值)存在差别:气体的相对分子质量越小,分子的运动速度越大。氢气的分子最轻,在相同温度下的运动速度最大。

这是科学的核心过程)作者说,许多观察都证实了这一点。就是在这时,他向我们介绍了本文开头的实验。这个实验向我们表明:氢气分子确实运动得比空气分子(学究的人会说:没有空气分子这种东西!)快得多。漏斗内的空气分子可以穿过气孔来到容器A,容器A里的氢气分子可以穿过气孔进入漏斗,但是,由于氢气分子速度比空气分子大很多(约为四倍),它从A向漏斗内的转移相对更快,因此,漏斗内气体分子的总数增加,压强增加(阿伏伽德罗定律)
把漏斗颈内的水压下去,并从漏斗口逃出。有人会想:有没有另一种可能性,氢气分子进入漏斗更快,是由于氢气分子更小?作者解释,氢气分子的长度约为2.3埃,氧气和氮气分子的长度约为3埃,这点差别对于扩散速度的差异不起什么作用,因为容器B上的气孔比它们大了几千倍。在理解了这一切之后,你是不是能够体会这个实验的美妙了?在解释完这个实验后,作者用一句话结束了这一节:矿井中的瓦斯会引起爆炸,人们用与这个实验类似的装置,检测矿井中的空气是否混进瓦斯
发表评论:
◎欢迎参与讨论,请在这里发表您的看法、交流您的观点。