在1873年的科学盛事中,著名学者麦克斯韦推出了划时代的科学巨著《电磁理论》,震撼了整个学术圈。这本著作的出现,不仅实现了物理学史上前所未有的统一大业,更系统、全面、完美地阐述了电磁场理论,从而为经典物理的基石增添了新的力量。麦克斯韦不仅预测了电磁波的潜在存在,他的这项预言还为现代无线通信的大门敲响了序曲。
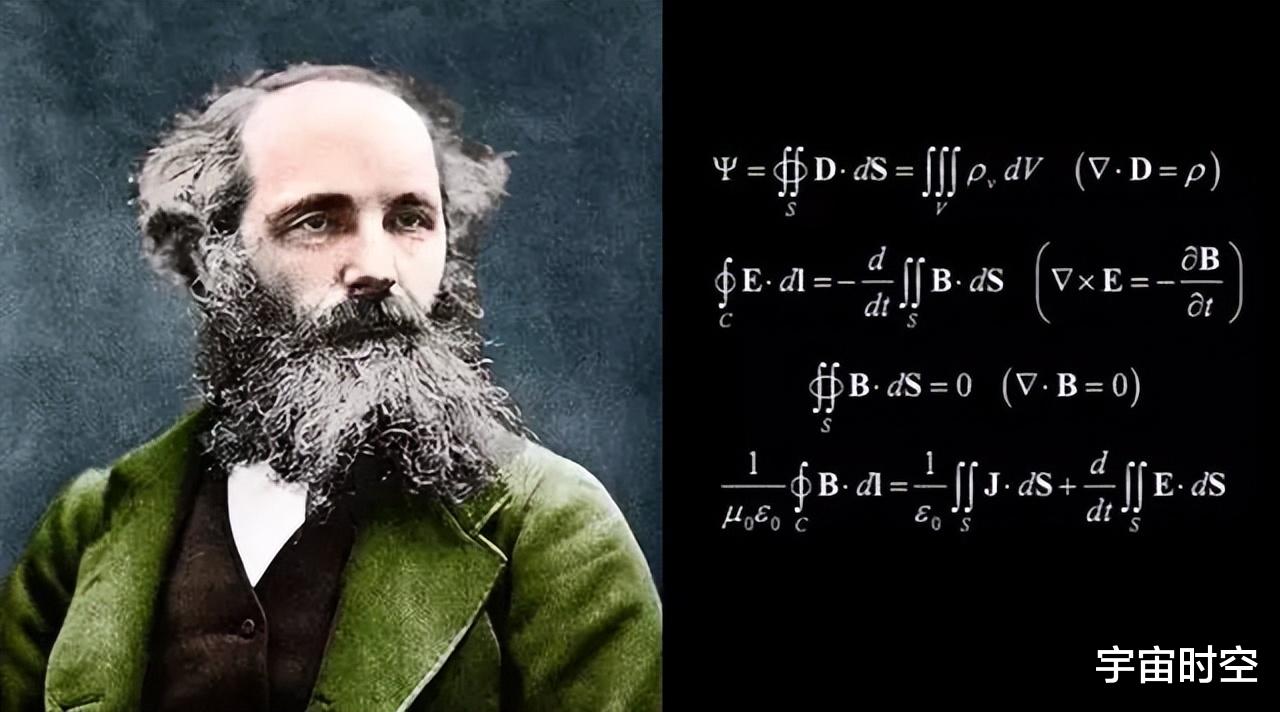
在麦克斯韦的理论中,电、磁、光三者得以统一,这是19世纪物理学领域最为辉煌的成就,亦是科学史上绝无仅有的伟大融合。可以毫不夸张地说,如果没有电磁学,现代电工学的诞生便无从谈起,也就没有今日我们所熟悉的现代文明。
麦克斯韦为了将电磁场理论从介质推广至空间,大胆地提出了一种假说:空间中存在一种被称作以太的动力学物质,它具有一定的密度,并拥有能量和动量。以太的动能展现了磁的特性,势能则体现了电的属性。它的动量被视为电磁最基础的量度,代表着电磁场的运动特性及传力的特征。1865年,他提出一组包含20个变量的20个方程式,即众所周知的麦克斯韦方程组。此外,他在1873年尝试用四元数来表示这些方程,但最终未能如愿以偿。
然而,在当时的科学界,麦克斯韦的理论并未得到广泛认可。如同18世纪科学家将牛顿学说奉为绝对真理一般,当时的人们尚未意识到麦克斯韦的学说价值。

由于过于辛勤地推广自己的电磁学理论,麦克斯韦终因劳累过度于1789年不幸离世,未能在有生之年完善自己的公式体系。
直到1884年,奥利弗·赫维赛德和约西亚·吉布斯采用矢量分析法重新表述了麦克斯韦的理论,我们现在所熟知的麦克斯韦方程组才最终确立。
奥利弗·赫维赛德同样具有传奇色彩,曾因猩红热导致耳聋,却凭借自学成就了一番伟业。他将麦克斯韦方程组从四元数转变为矢量形式,从而将原先的20条方程精简为4条微分方程。
而吉布斯为化学热力学奠定了基础,他创立了向量分析,并将其引入数学物理领域,进一步将麦克斯韦方程组引入物理光学研究。这两位科学巨匠携手将我们现在所见的麦克斯韦表达形式完善至极。
麦克斯韦方程组精确地描绘了电磁场的特性及其相互作用的机理。如此一来,麦克斯韦便将错综复杂的物理现象归纳为一套统一而完整的学说。麦克斯韦方程在理论与应用科学领域的广泛应用已逾一个世纪,它构成了现代文明发展的基石。

麦克斯韦方程组通常有积分形式与微分形式之分,其中H代表磁场强度,D为电通量密度,E为电场强度,B为磁通密度,J为电流密度,ρ为电荷密度。在采用其他单位制度时,方程中的某些项会出现一常数因子,例如光速c等。

积分形式的麦克斯韦方程组是描述电磁场在某一体积或面积内的数学模型。其中第一个公式是由安培环路定律推广而来的全电流定律,第二个公式是法拉第电磁感应定律的表达,第三个公式显示了磁通的连续性原理,而最后一个公式则体现了高斯定律。
麦克斯韦方程组的积分形式既描绘了电场的性质,也揭示了磁场的特性,并且描述了变化磁场激发电场以及传导电流和变化电场激发磁场的规律。
它反映了空间某区域电磁场量(D、E、B、H)与场源(电荷q、电流I)之间的关系。在电磁场的实际应用中,我们经常需要了解空间各点的电磁场量与电荷、电流的关联。而微分形式则是麦克斯韦方程组积分形式在数学表达上的一种转变。

麦克斯韦方程组构建了电动力学的基石,但与牛顿的经典力学产生了冲突。麦克斯韦建立的电动力学表明,光速在不同的惯性系中保持不变,这个结论与经典力学的伽利略变换产生了矛盾。
伽利略变换是经典力学中描述两个仅以恒定速度相对移动的参考系之间变换的方法,属于一种被动态的变换。它构建了经典力学的时空观念。
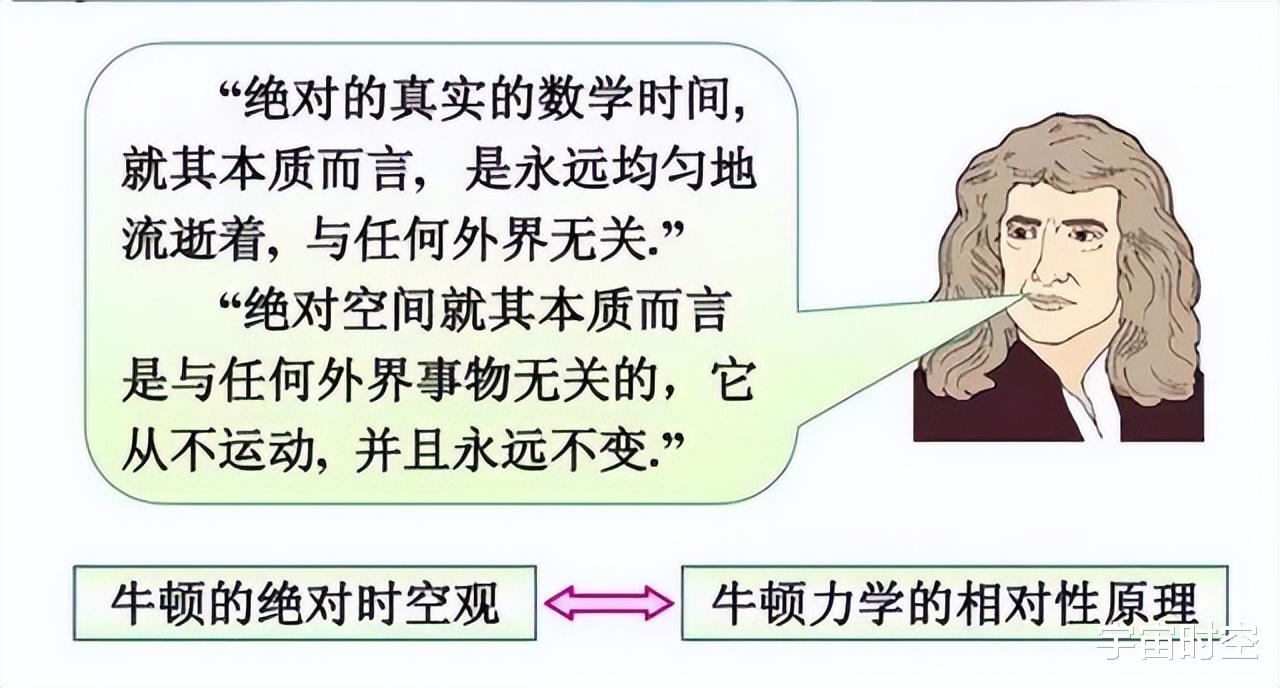
伽利略变换假定,在同一参照系中,两个事件同时发生,在其他惯性系中,这两个事件也必然同时发生。时间间隔的测量是绝对的,长度的测量也是绝对的,经典力学定律在所有惯性参考系中的数学形式保持不变,也就是说,所有惯性系都是等价的(相对性原理)。伽利略变换还构建了经典力学中绝对的时空观,时间和空间与参考系的运动状态无关,且互不联系,是绝对的。
这种绝对的时空观与麦克斯韦创建的电动力学产生了冲突。当我们将伽利略变换应用于描述电磁现象的麦克斯韦方程组时,会发现其形式并不保持不变,即在伽利略变换下,麦克斯韦方程组或电磁现象规律不满足相对性原理。
由麦克斯韦方程组,我们可以得到电磁波的波动方程,其解出的真空中的光速为一常数。根据经典力学的时空观,这个结论只在特定的惯性参照系——以太中成立。
一句话总结:电磁现象所遵循的麦克斯韦方程组不遵守伽利略变换。

牛顿认为,引力甚至电磁力是在以太中传播的。受到经典力学思想的影响,科学家们假定宇宙中充满了一种称为以太的物质,他们普遍认为以太是传播电磁波和光的媒介。在经典物理学中,将这种无处不在的“以太”视为绝对惯性系,其他参照系中测量到的光速是相对于以太参照系中光速与观察者所在参照系的速度矢量叠加的结果。

为了解决这个矛盾,洛伦兹建立了洛伦兹变换。洛伦兹提出,洛伦兹变换是观察者在不同惯性参照系间进行测量时所采用的转换关系,在数学上表现为一组方程。该变换同样是基于以太存在的前提,基于光速不变原理,在任何惯性参照系中,光速都保持相同数值。

1887年的迈克耳孙-莫雷实验旨在证明以太的存在。如果能确定以太与地球的相对速度,即以太漂移速度,就能证明以太的存在。然而,实验未能检测到地球相对于以太参照系的运动速度,得出地球相对以太不运动的结论。后续的其他实验也得到了同样的结果。
洛伦兹为了在不放弃光速与参照系无关这一观点的前提下拯救以太假设,抛弃了空间间隔和时间间隔与参照系无关的绝对观念。在他看来,常驻以太参照系是基本参照系,在这个参照系中,时间均匀流逝,空间均匀且各向同性。实际参照系都相对该基本参照系运动。

根据洛伦兹的设想,观察者相对于以太以一定速度运动时,长度在运动方向上发生收缩,以此抵消不同方向上由于光速差异所造成的影响,从而解释了迈克耳孙-莫雷实验的零结果。

洛伦兹变换在一定程度上调和了经典力学与电动力学之间的矛盾,为伽利略变换提供了一个适用领域,从而解释了为何伽利略变换下麦克斯韦方程组或电磁现象规律不满足相对性原理。

然而,洛伦兹变换毕竟是为了拯救错误的以太假说而提出的,在调和经典力学与电动力学之间的矛盾上仍存在许多问题。在相对论出现之前,洛伦兹从存在绝对静止以太的观念出发,考虑物体运动发生收缩的物质过程得出洛伦兹变换。在洛伦兹的理论中,变换所引入的量仅被视为数学上的辅助手段,并不包含相对论的时空观。
爱因斯坦洞察到解决这种不协调状况的关键在于同时性的定义。爱因斯坦认为,既然光速不变,那么作为静止参照系的以太便没有存在的理由。于是,他摒弃了静止参照系以太、光速不变原理以及狭义相对性原理作为基本假设,建立了狭义相对论。爱因斯坦基于现实观察,着眼于修改运动、时间、空间等基本概念,重新推导出洛伦兹变换,并赋予其崭新的物理内容,以解释迈克尔逊-莫雷实验和光速不变。爱因斯坦的洛仑兹变换指的是纯数学的空间缩短,不再是组成量杆的带电粒子距离的缩短,且这种空间缩短不具有任何实质性的物理意义。
在狭义相对论的架构中,洛伦兹转换式乃是核心的公式,它导出了狭义相对论的种种运动结论和时空特性。这些结论和特性包含了相对性原理、长度收缩、时间膨胀、速度合成公式以及相对论版的多普勒效应等,全部可以从洛伦兹转换式中推演出来。
秉持光速不变的原理,我们得知在任何惯性参考系中,光速都维持不变的值。在此基础上以及相对性原理的指导下,
在狭义相对论中,时空的三个维度与时间轴合一,形成一个四维的时空结构。不同惯性参考系之间的变换公式,在数学形式上与洛伦兹转换式如出一辙。
这样一来,古典力学与电动力学间的矛盾得到完全的解决。如果一个物体的速度v远远小于光速с,且被观测物体的速率也远低于光速,则洛伦兹转换在效果上便与伽利略公式趋于一致。对于常见的力学现象,伽利略公式绰绰有余。但若涉及运动物体的电磁现象,哪怕物体速度较光速而言微不足道,由于电磁相互作用传递的速度为光速,洛伦兹转换的使用变得必不可少。

自笛卡尔将以太引入科学领域,赋予其力学属性,认定所有物体间的作用力皆透过以太这个媒介传播,以太学说将近束缚了物理学家三百年。他们在探索各种物理现象、规律、法则时,无一不将以太的存在纳入考虑。然而,爱因斯坦的狭义相对论终结了以太的迷思,明确指出在所有惯性参考系中,光速的测量值是不变的,从而否决了以太(绝对静止参考系)的必要,这不仅是对经典物理学根基的一次震撼,也是现代物理学开篇的序幕。

自此以后,相对论应用于高速运动与微观世界;经典力学则主宰着宏观尺度与低速领域的探索;而电动力学在电磁现象中,发挥着不可或缺的作用。三者交相辉映,共同编织出物理学的多彩画卷。
发表评论:
◎欢迎参与讨论,请在这里发表您的看法、交流您的观点。