你们很难想象你一生中有几个娃,居然与你们家水龙头中流出的水滴有着千丝万缕的联系。今天就来讲一个本世纪最重要的发现。这一切呢,还要从一个不正经的教授讲起。
在美国有这样一个教授,这个人脑回路清奇,总是会用一些类似于整蛊的奇奇怪怪的方法来带研究生。这位教授得名不正经教授。有一次,他给他的研究生们搞了一个小比赛,叫做“优生大挑战”。他让学生们三五成群,自己组成小组,在相同的实验舱里面互相PK。这个项目,就是看谁能培养出最多同时存活的老鼠,谁就是冠军。说到这儿,有的朋友可能会想到一个著名的老鼠乌托邦的实验。
就在1968年的时候,有一位叫约翰·卡尔宏的科学家,他将四对老鼠放入了一个叫做“老鼠乌托邦”的特质实验舱中。该实验舱底部面积为2.7平方米,四边围栏高1.4米,每一边都有四个直立网状的隧道。这些隧道通往各个居室、食物漏斗以及饮水分配处。也就是说,在这套实验舱中,老鼠不会面临食物、水源和住房短缺的问题。同时,还给这些老鼠配备了清洁员,让整个群体不会产生疫病。所以,这个实验舱除了生存空间对老鼠的繁殖有限制之外,在其他方面都没有对老鼠有任何的限制。虽然生存空间有所限制,但也足够3840只老鼠在里面存活。
起初,老鼠的数量迅速增长。在实验开展后的第315天,老鼠的数量达到了620只。100天之后,老鼠的数量来到了2000。在这个时候,转折点出现了,老鼠的数量不再继续快速上涨,而是趋于平缓。
到达第600天的时候,这个“老鼠乌托邦”的特制实验室中存活的老鼠数量为2200只。而这2200只便是那次实验所达到的最大数量。从那之后,老鼠的数量开始减少。这一点让很多科学家感到不解,因为实验舱设计出来的生存空间明明足够3840只老鼠共同生存。然而,老鼠的种群数量却突破不了2200只这个界限。
后来,实验的发起人卡尔宏出来解释说,这些老鼠由于内卷,他们的生存空间被同类占领了,很多强势的老鼠圈更多的领地,来压榨那些比较弱的老鼠,导致了很多老鼠在精神和心理上都出现了问题。这些出现问题的老鼠表现出了很多异常的行为,比如在断奶前就将幼稚遗弃,还有伤害幼崽,雄性变得更爱梳妆打扮,同性性行为增加,雌性出现了明显的攻击性行为等等。
当时的卡尔宏觉得自然界有一双无形的手,以一种我们人类还理解不了的方式巧妙地控制各个种群的数量。这个不正经的教授便在他的研究生中开展了一个“优生大挑战”的比赛,想看看有没有学生能够突破这双手的限制。
于是,“优生大挑战”开始后,有的学生研究食物,有的研究药物,有的研究老鼠的运动,还有的直接研究老鼠的基因。同学们从各个维度来提升老鼠的生育率和存活率。经过一年半的研究、老鼠培养、再研究再培养,最终一组研究老鼠基因的同学通过基因筛选培育出了既健康又多的老鼠。最后,他们在实验舱中使这些老鼠达到了同时存活最多的数量。
不正经教授将优胜奖颁给了这一组同学。但此刻,他开始不正经了,说在这个优胜奖之上还有一个特等奖,要颁给那些创造惊喜和意外的同学们。这次,就有一组同学创造了这样一个惊喜和意外。这又是怎么样的一个意外呢?值得这样一个特等奖。
一般的小组在培养老鼠时,对老鼠的数量与时间的关系是这样的:到最后,这条曲线几乎是平的。这也很好解释,当你的各种资源不足以支撑人口上涨时,人口的数量就会维持在一个水平,即所谓的当前的人口均衡点。但是在这一组,却出现了意外,他们的人口均衡点出现了一个上下横跳的迹象。为什么会这样呢?
于是,他们开始用计算机模拟整个过程。当时采用的算法模型是澳大利亚科学家罗伯特·梅总结提炼的一个人口增长模型。这个模型表示为:
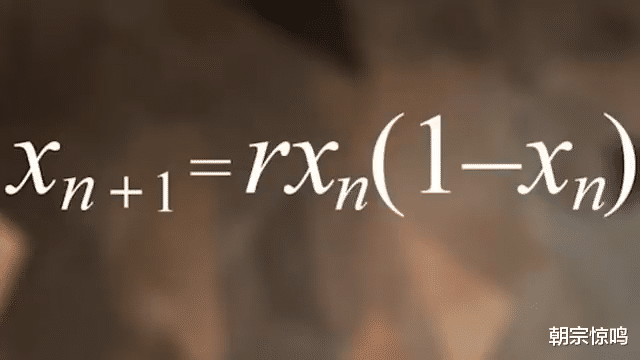
其中,等号左边表示下一代人口,r表示人口增长率。如果第一代有两个人,第二代变成了四个,那么人口增长率就是2。
模拟开始时,他们发现改变第一代少数的数量并不会影响均衡点的位置。于是,他们开始减小人口增长率r的值。均衡点的位置终于开始变化,r值越小,均衡点的位置就越低。当r值小于1的时候,均衡点变成了零,也就是说,当人口增长率小于一时,这个种群最终会走向灭亡。
这也很好理解,就比如大家结婚后生一个小孩,你的人口增长率就是小于一。这样,事实上,人口必然越来越少。所以,他们开始增加r的值,让人费解的一件事情就发生了。为了方便观察,我们把x和均衡点的关系单独放在了右边的表中。在这个过程中,我们不难发现,在0-1这个区间内,种群最终会走向灭亡。所以,均衡点的值一直在零这个位置。
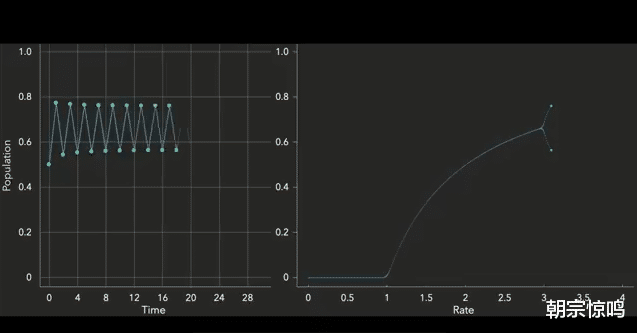
当r大于一时,均衡点的值开始逐步攀升,并且越大,均衡点的值也越大。但是接下来诡异的一幕就发生了,当r差不多到达三左右的时候,右边的图形出现了分叉。从左边我们可以看到均衡点,终于出现了小波动。他们当时的情况就是上下横跳的一个均衡点。
这一表示,可能你这一代人是10亿人,下代人可能就只有5亿了。然后,又变成10亿,在下一代又变成5亿,这就感觉人口的变化是以两个点为周期在进行着变化。
从图形上我们也可以看到这个人口均衡点,它是在两个点之间来回横跳。随着r值再增大,我们会发现这个图像又再次分叉,这一次均衡点是在四个点之间上下横跳。出现分叉的时间也开始缩短了,8个叉、16个叉、32个叉、64个叉,当r增加到3.57左右的时候,混沌就出现了。
这个时候,左边的均衡点几乎已经可以说是毫无规律可言的在跳动。后面的科学家也验证过,这些均衡点的分布可以说是完全随机的。正当你以为随着r的增加,这种无序随机的情况会继续下去的时候,这个反转来了。就当r差不多达到3.83的时候,他的秩序和规律突然一下又回来了,均衡点突然之间又开始在三个点之间来回横跳。
在这个分叉的分析图中,他还隐藏着一个和黄金分割类似的奇特现象。这个现象由科学家费根鲍勃发现,就是这次分叉的长度和下次分叉的长度的比值几乎是一个定值,约等于4.669。这个数对现代复杂科学具有深远意义的费根鲍姆常数。

当科学家们用频率逐渐升高的闪光灯来对人眼进行照射时,人眼对这些闪光灯的生物电反应就会呈现出这样一个分叉图。后来,人们直接把这种现象称之为倍周期分叉及混沌现象。科学家在生物神经放电的模式中也发现了这个现象。随后,研究经济、电流、交通流的学者相继在各自的领域发现了这个现象。甚至厨房里从水龙头滴出来的水滴也会出现倍周期分叉和混沌现象。这个自然界中不同事物都普遍出现的现象,可以说是我们宇宙终极规律的缩影。
如果我们能够破解并解读这种现象和规律,便可以紧密观察水龙头中流出的水滴,预测未来人口会如何发展,预测你的心跳何时会出现心律不齐,以及预测何时何地会出现交通事故。虽然这听起来确实很让人兴奋,但是事实情况:总是解开一个谜题的往往是另外一个谜题。
◎欢迎参与讨论,请在这里发表您的看法、交流您的观点。