韦德体育注册老虎机 洛伦兹变换，狭义相对论的核心，也是电动力学与经典力学的调和者

在物理学的历史长河中，19世纪下半叶无疑是一个丰收的季节。在这一时期，一个名叫詹姆斯·克拉克·麦克斯韦的苏格兰物理学家，站在了巨人的肩膀上，将此前分散的电磁学知识汇集成一个宏伟的理论体系——麦克斯韦方程组。这一方程组不仅完美地统一了电与磁，而且预言了电磁波的存在，为现代无线通信奠定了基础。

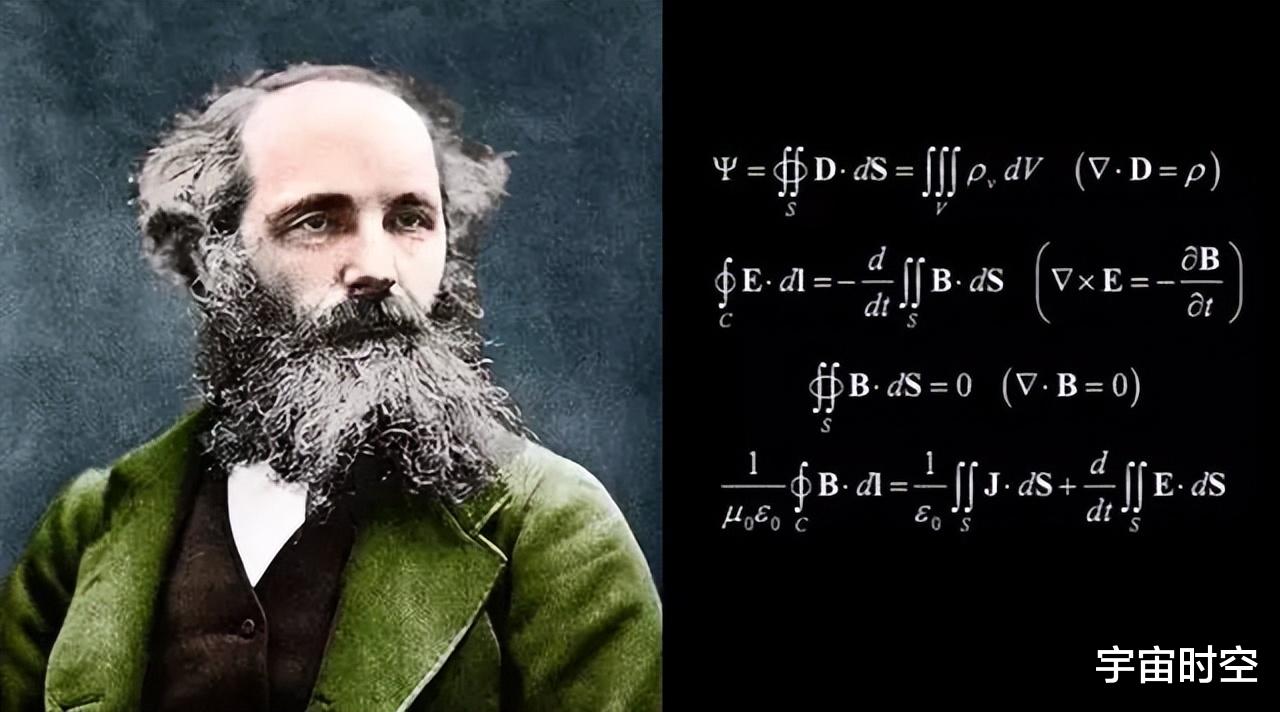
麦克斯韦方程组的积分形式和微分形式，准确描绘了电磁场的特性及其相互作用的关系，将混乱纷纭的现象归纳成为一种统一完整的学说。这一理论的提出，无疑是物理学史上的一次巨大飞跃，它标志着经典物理学的一个新高峰。然而，这座高峰的背后，却隐藏着一片令人困惑的迷雾。

当麦克斯韦的电磁理论与牛顿的经典力学相遇时，矛盾便随之产生。根据经典力学的伽利略变换，时间和空间是绝对的，而在电磁理论中，光速却是一个不变的常数。这意味着，电磁现象的规律在不同的惯性系中应当有所不同，这与伽利略变换所描述的经典力学时空观产生了冲突。电磁学与经典力学之间的这一矛盾，成为了物理学进一步发展的障碍。

要理解这一矛盾，我们需要回到伽利略变换本身。伽利略变换是描述在两个只以均速相对移动的参考系之间变换的方法，属于一种被动态变换。这一变换构建了经典力学的时空观，认为时间和空间均与参考系的运动状态无关，是绝对的。

伽利略变换的核心在于，它假设在同一参照系里，两个事件同时发生，在其他惯性系里，这两个事件也一定同时发生。这种观点意味着，时间间隔的测量是绝对的，长度测量也具有绝对性。因此，经典力学定律在任何惯性参考系中数学形式不变，所有惯性系都是等价的。换言之，伽利略变换体现了一种绝对时空观，时间和空间是不相联系的，是绝对的。

然而，当这一观念应用到麦克斯韦的电磁理论时，却出现了问题。因为麦克斯韦方程组描述的电磁现象表明，光速在不同惯性系中是不变的。这意味着，如果按照伽利略变换的假设，电磁波的速度应当在不同的惯性系中有所不同，但实际情况并非如此。电磁现象所遵从的麦克斯韦方程组不服从伽利略变换，这揭示了经典力学的绝对时空观与电磁学的冲突。

面对电磁学与经典力学之间的矛盾，荷兰物理学家亨德里克·洛伦兹进行了一系列尝试，试图调和这两大理论。洛伦兹的变革始于对迈克尔逊-莫雷实验的解释，该实验旨在探测地球相对于以太的运动速度，但实验结果却是零。这一结果对以太存在的假设提出了质疑。

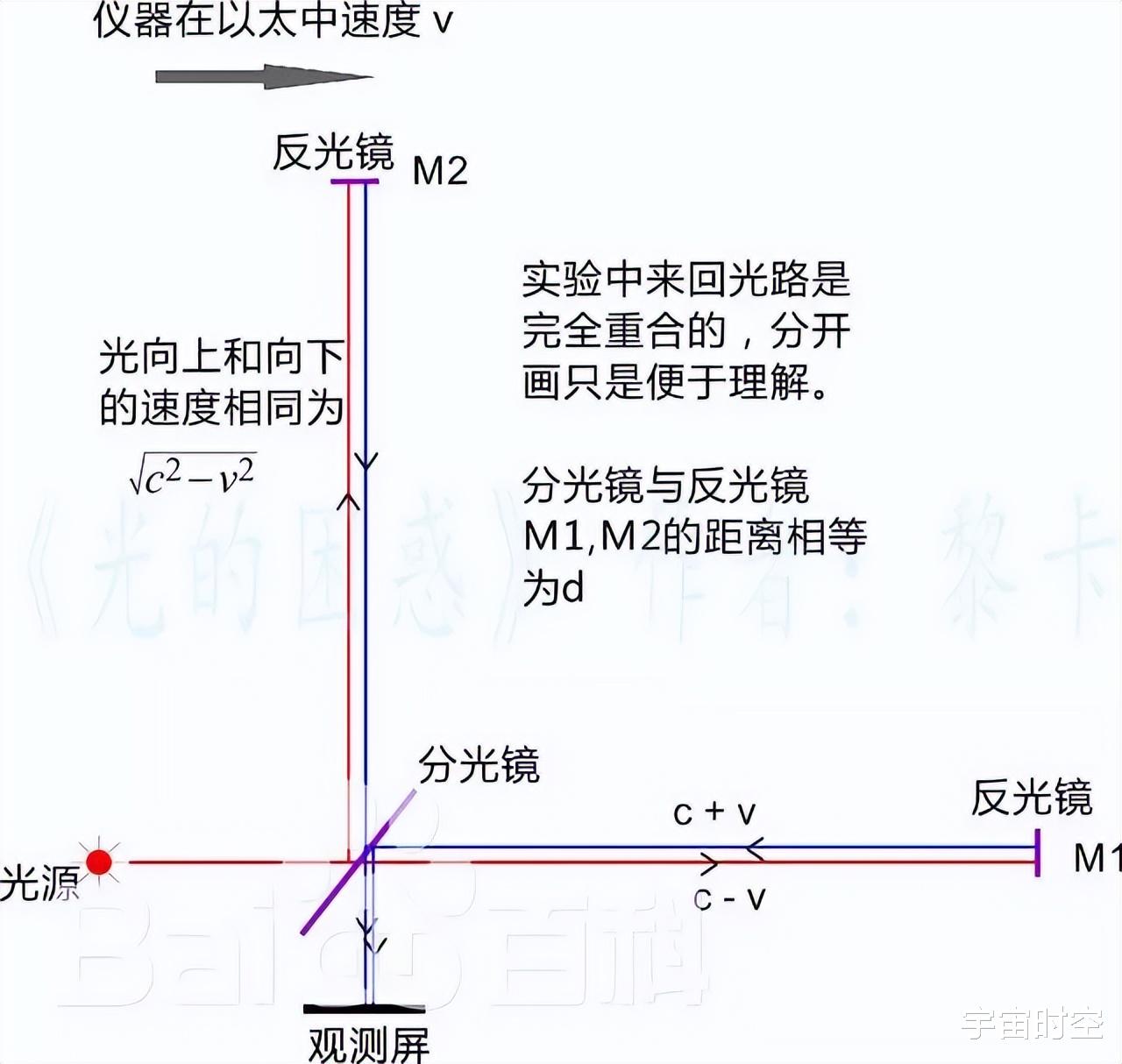
洛伦兹为了解决这一难题，提出了一套新的变换方程组——洛伦兹变换。他的理论认为，光速在所有惯性系中都是不变的，而时间和空间则会随观察者的运动状态而变化。这一理论在数学上表现为一套方程组，它修正了伽利略变换，使得电磁现象的规律在不同的惯性系中保持不变。

洛伦兹变换的提出，一定程度上调和了经典力学和电动力学之间的矛盾，给了伽利略变换一个适用的领域。它解释了为什么在伽利略变换下，麦克斯韦方程组或电磁现象规律不满足相对性原理。然而，洛伦兹变换毕竟是为了拯救错误的以太假说而提出的，在调和经典力学与电动力学之间的矛盾上还存在许多的问题。

在洛伦兹的理论中，变换所引入的量仅仅看作是数学上的辅助手段，并不包含相对论的时空观。洛伦兹认为，存在一个基本的惯性参照系——常驻以太参照系，在这个参照系中，时间是均匀流逝的，空间是均匀的，各向同性的。任何实际参照系都相对于这个基本参照系运动着。尽管洛伦兹的理论在当时被广泛接受，但它并未能彻底解决电磁学与经典力学之间的冲突。

爱因斯坦在洛伦兹变换的基础上，进行了更为深刻的革新。他洞察到，同时性的定义是解决电磁学与经典力学之间不协调状况的关键。爱因斯坦认为，既然光速不变，作为静止参考系的以太就没有存在的理由。于是，他抛弃了静止参考系以太的概念，以光速不变原理和狭义相对性原理为基本假设，建立了狭义相对论。

狭义相对论的建立，彻底颠覆了人们对时间和空间的传统认识。在狭义相对论中，空间和时间不再是相互独立的，而是一个统一的四维时空整体。不同惯性参照系之间的变换关系式与洛伦兹变换在数学表达式上是一致的。这意味着，爱因斯坦的洛伦兹变换不仅仅是数学上的变换，它还包含了深刻的物理意义。

狭义相对论认为，相对于任何惯性参考系，光速都具有相同的数值。在这一理论下，时间和空间的概念被重新定义，同时性的相对性、长度收缩、时间延缓等概念相继提出。这些结论可以直接从洛伦兹变换中得出，而这些变换不再是描述空间和时间独立变化的数学工具，而是反映了时空本身的性质。

爱因斯坦的狭义相对论剿灭了以太这一概念，证明光速在不同惯性系和不同方向上都是相同的，由此否认了以太（绝对静止参考系）的存在，从而动摇了经典物理学基础。狭义相对论的建立，不仅解决了电磁学与经典力学之间的矛盾，也为物理学的进一步发展开辟了新的道路。

洛伦兹变换在现代物理中占据着举足轻重的地位，它不仅是狭义相对论的数学表达，更是现代物理的基石之一。在狭义相对论中，洛伦兹变换揭示了时间和空间的相对性，为高速微观领域的物理现象提供了理论基础。

狭义相对论认为，所有物理规律在所有惯性系中都应该具有相同的形式。这一原理要求，任何物理量的测量结果，都应该通过洛伦兹变换来在不同的惯性系之间进行转换。因此，洛伦兹变换成为了连接不同惯性系的桥梁，它在狭义相对论的运动学结论和时空性质中扮演了核心角色。

同时性的相对性、长度收缩、时间延缓等狭义相对论效应，都可以通过洛伦兹变换得到明确的数学描述。例如，时间延缓效应表明，在高速运动的参照系中，时间流逝的速度会变慢。这一效应可以通过洛伦兹变换中的时间膨胀因子来体现。同样，长度收缩效应表明，在高速运动的参照系中，物体的长度会在运动方向上缩短。这一效应则可以通过洛伦兹变换中的长度收缩因子来描述。

在现代物理的其他领域，如量子力学和广义相对论中，洛伦兹变换同样发挥着重要作用。在量子场论中，洛伦兹变换是描述基本粒子相互作用的基本工具。而在广义相对论中，洛伦兹变换则被推广为更加复杂的数学结构，用以描述引力场对时空的影响。

总而言之，洛伦兹变换不仅仅是狭义相对论的核心内容，它更是现代物理理论框架中不可或缺的一环。它将电磁学与经典力学巧妙地结合在一起，为我们理解自然界的深层次规律提供了强有力的数学工具。